Entropy scaling of pure substances¶
Goal¶
Learn how to compute dynamic properties (viscosity in this example)
Compare substance specific parameters against homo-segmented group contribution
Compare viscosity to NIST data (generated in NIST’s webapp)
Import needed packages¶
[1]:
from feos.pcsaft import *
from feos.eos import *
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
import si_units as si
sns.set_context("talk")
sns.set_palette("Dark2")
sns.set_style("ticks")
PC-SAFT (individual component parameters)¶
First, we read parameters adjusted to hexane saturation pressure and liquid densities (for the regular SAFT parameters) and to viscosity (for correlation).
[2]:
parameters = PcSaftParameters.from_json(
["hexane"], "../parameters/pcsaft/loetgeringlin2018.json"
)
parameters
[2]:
component |
molarweight |
\(m\) |
\(\sigma\) |
\(\varepsilon\) |
\(\mu\) |
\(Q\) |
\(\kappa_{AB}\) |
\(\varepsilon_{AB}\) |
\(N_A\) |
\(N_B\) |
\(N_C\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
hexane |
86.177 |
3.0576 |
3.7983 |
236.77 |
0 |
0 |
0 |
PC-SAFT homo-GC¶
For transparency, we build parameters by hand. You can read a detailed explanation about PC-SAFT parameters in the “working with parameters” tutorial.
[3]:
hexane = ChemicalRecord(
identifier=Identifier(
cas="110-54-3",
name="hexane",
iupac_name="hexane",
smiles="CCCCCC",
inchi="InChI=1/C6H14/c1-3-5-6-4-2/h3-6H2,1-2H3",
formula="C6H14"
),
segments=['CH3', 'CH2', 'CH2', 'CH2', 'CH2', 'CH3']
)
ch3 = SegmentRecord(
'CH3',
molarweight=15.0345,
model_record=PcSaftRecord(
m=0.61198, sigma=3.7202, epsilon_k=229.90,
viscosity=[-8.6878e-3, -1.7951e-1, -12.2359e-2, -0.01245]
)
)
ch2 = SegmentRecord(
'CH2',
molarweight=14.02658,
model_record=PcSaftRecord(
m=0.45606, sigma=3.8900, epsilon_k=239.01,
viscosity=[-0.9194e-3, -1.3316e-1, -4.2657e-2, -0.01245]
)
)
segment_records = {r.identifier: r for r in [ch3, ch2]}
def from_segments(chemical_record, segment_records):
m = 0
s3 = 0
eps = 0
mw = 0
viscosity = np.zeros(4)
for s in chemical_record.segments:
segment = segment_records[s]
mw += segment.molarweight
m += segment.model_record.m
s3 += segment.model_record.m * segment.model_record.sigma**3
eps += segment.model_record.m * segment.model_record.epsilon_k
v = segment.model_record.viscosity
viscosity += np.array([
v[0] * segment.model_record.m * segment.model_record.sigma**3,
v[1] * segment.model_record.m * segment.model_record.sigma**3,
v[2],
v[3]
])
viscosity[1] /= s3**0.45
# We have to shift the "A" parameter because the implemented reference
# is eta_CE according to eq. 3 of Loetgerin-Lin (2018)
# A = A(GC) + log(sqrt(1/m)) = -log(m)/2
viscosity[0] += np.log(np.sqrt(1/m))
saft_record = PcSaftRecord(m, np.cbrt(s3 / m), eps / m, viscosity=viscosity)
return PureRecord(chemical_record.identifier, mw, saft_record)
Build equations of state¶
We instantiate an equation of state for each parameter set. saft uses substance specific parameters while saft_gc uses homo GC parameters both for SAFT as well as correlation parameters.
[4]:
parameters_gc = PcSaftParameters.new_pure(from_segments(hexane, segment_records))
saft_gc = EquationOfState.pcsaft(parameters_gc)
saft = EquationOfState.pcsaft(parameters)
m_gc = parameters_gc.pure_records[0].model_record.m
m = parameters.pure_records[0].model_record.m
Compare parameters¶
[5]:
print("Substance specific: ", parameters.pure_records[0].model_record.viscosity)
print("Segments : ", parameters_gc.pure_records[0].model_record.viscosity)
Substance specific: [-1.2035, -2.5958, -0.4816, -0.0865]
Segments : [-1.2034921145837285, -2.536713016411593, -0.415346, -0.0747]
Compare methods to NIST data (T = 450 K)¶
We will compute the residual entropy, viscosity and logarithmic reduced viscosity and compare to literature data (for which the entropy is computed with parameters fitted to the component, not GC).
[6]:
literature = pd.read_csv("data/hexane_nist.csv", delimiter="\t")
literature.head()
[6]:
| Temperature (K) | Pressure (MPa) | Density (mol/m3) | Volume (m3/mol) | Internal Energy (kJ/mol) | Enthalpy (kJ/mol) | Entropy (J/mol*K) | Cv (J/mol*K) | Cp (J/mol*K) | Sound Spd. (m/s) | Joule-Thomson (K/MPa) | Viscosity (Pa*s) | Therm. Cond. (W/m*K) | Phase | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 450.0 | 0.01 | 2.6774 | 0.373500 | 45.229 | 48.964 | 154.33 | 193.37 | 201.76 | 212.47 | 11.204 | 0.000009 | 0.029374 | vapor |
| 1 | 450.0 | 0.11 | 29.9840 | 0.033351 | 45.065 | 48.734 | 134.03 | 193.94 | 203.09 | 209.04 | 11.510 | 0.000009 | 0.029276 | vapor |
| 2 | 450.0 | 0.21 | 58.3290 | 0.017144 | 44.896 | 48.496 | 128.27 | 194.53 | 204.55 | 205.48 | 11.842 | 0.000009 | 0.029196 | vapor |
| 3 | 450.0 | 0.31 | 87.8260 | 0.011386 | 44.720 | 48.249 | 124.64 | 195.15 | 206.15 | 201.76 | 12.207 | 0.000009 | 0.029136 | vapor |
| 4 | 450.0 | 0.41 | 118.6100 | 0.008431 | 44.536 | 47.992 | 121.90 | 195.80 | 207.93 | 197.87 | 12.608 | 0.000010 | 0.029098 | vapor |
We loop through experimental data, read temperature, pressure and the phase (liquid or vapor) and generate State objects for the experimental conditions. Then, we compute the residual molar entropy and the logarithmic reduced viscosity.
[7]:
results = []
for i, row in literature.iterrows():
t = row['Temperature (K)'] * si.KELVIN
p = row['Pressure (MPa)'] * si.MEGA * si.PASCAL
viscosity_lit = row['Viscosity (Pa*s)'] * si.PASCAL * si.SECOND
# literature
state = State(saft, temperature=t, pressure=p, total_moles=si.MOL, density_initialization=row.Phase)
s = state.molar_entropy(Contributions.Residual)
results.append(
{
"pressure": p / si.MEGA / si.PASCAL,
"s*_res/m": s / si.RGAS / m,
"viscosity": viscosity_lit / (si.PASCAL * si.SECOND),
"ln_viscosity_reduced": np.log(viscosity_lit/ state.viscosity_reference()),
"source": "literature",
"rel.dev.": 0.0
}
)
# individual parameters
viscosity = state.viscosity()
ln_viscosity_reduced = state.ln_viscosity_reduced()
results.append(
{
"pressure": p / si.MEGA / si.PASCAL,
"s*_res/m": s / si.RGAS / m,
"viscosity": viscosity / (si.PASCAL * si.SECOND),
"ln_viscosity_reduced": ln_viscosity_reduced,
"source": "saft",
"rel.dev.": (viscosity - viscosity_lit) / viscosity_lit * 100
}
)
# homo GC
state = State(saft_gc, temperature=t, pressure=p, total_moles=si.MOL)
s = state.molar_entropy(Contributions.Residual)
viscosity = state.viscosity()
ln_viscosity_reduced = state.ln_viscosity_reduced()
results.append(
{
"pressure": p / si.MEGA / si.PASCAL,
"s*_res/m": s / si.RGAS / m_gc,
"viscosity": viscosity / (si.PASCAL * si.SECOND),
"ln_viscosity_reduced": ln_viscosity_reduced,
"source": "homo-GC",
"rel.dev.": (viscosity - viscosity_lit) / viscosity_lit * 100
}
)
# gather everything in a data frame
data = pd.DataFrame(results)
data.head()
[7]:
| pressure | s*_res/m | viscosity | ln_viscosity_reduced | source | rel.dev. | |
|---|---|---|---|---|---|---|
| 0 | 0.01 | -0.000526 | 0.000009 | -1.170829 | literature | 0.000000 |
| 1 | 0.01 | -0.000526 | 0.000009 | -1.202136 | saft | -3.082130 |
| 2 | 0.01 | -0.000531 | 0.000009 | -1.202146 | homo-GC | -4.154342 |
| 3 | 0.11 | -0.005862 | 0.000009 | -1.172124 | literature | 0.000000 |
| 4 | 0.11 | -0.005862 | 0.000009 | -1.188299 | saft | -1.604523 |
[8]:
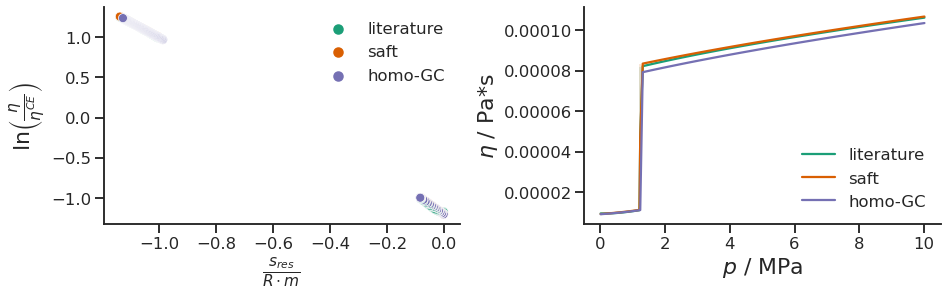
fig, ax = plt.subplots(1, 2, figsize=(15, 4), gridspec_kw={'wspace': 0.35})
sns.scatterplot(data=data, x='s*_res/m', y='ln_viscosity_reduced', hue='source', ax=ax[0]);
ax[0].set_xlabel(r"$\frac{s_{res}}{R \cdot m}$", fontsize=22)
ax[0].set_ylabel(r"$\ln\left(\frac{\eta}{\eta^{CE}}\right)$", fontsize=22);
ax[0].legend(frameon=False)
sns.lineplot(data=data, x='pressure', y='viscosity', hue='source', ax=ax[1]);
ax[1].set_xlabel(r"$p$ / MPa", fontsize=22)
ax[1].set_ylabel(r"$\eta$ / Pa*s", fontsize=22);
ax[1].legend(frameon=False)
sns.despine()
[9]:
# check mean absolute relative deviation in percent
mard = data.groupby('source')['rel.dev.'].apply(lambda x: np.mean(np.abs(x)))
print('Viscosity hexane compared to NIST data at T = 450 K')
print(f'MARD (individual): {mard.saft:.2f} %')
print(f'MARD (homo-GC) : {mard["homo-GC"]:.2f} %')
Viscosity hexane compared to NIST data at T = 450 K
MARD (individual): 0.81 %
MARD (homo-GC) : 3.70 %