Surface tension using PC-SAFT Helmholtz energy functionals

Goal of this notebook

• Learn how to compute the surface tension for a planar interface using the PC-SAFT functionals.

• Learn about the SurfaceTensionDiagram that allows convenient calculation of multiple surface tensions.

from feos.si import *
from feos.pcsaft import *
from feos.dft import *

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import seaborn as sns

sns.set_context("talk")
sns.set_palette("Dark2")
sns.set_style("ticks")

colors = sns.color_palette("Dark2", 2)

Water parameters for PC-SAFT

In this example we will calculate surface tensions for water using the 2B association scheme. The parameters that we use, were adjusted to vapor pressures, liquid densities and surface tensions. Parameters are available here.

# Equation of state object.
parameters = PcSaftParameters.from_json(
    ['water_2B'],
    '../parameters/pcsaft/rehner2020.json'
)
pcsaft = HelmholtzEnergyFunctional.pcsaft(parameters)

Let’s first compute the critical point. We will make use of the critical temperature later.

cp = State.critical_point(pcsaft)
cp

temperature	density
677.34347 K	18.70466 kmol/m³

As you can see, the model overestimates the critical temperature.

Surface tension for single VLE

To compute the surface tension, three steps are needed.

1. We need to compute the vapor liquid equilibrium (VLE) either at given temperature or pressure.

2. Then, we need to initialize a density profile. We will use a hyperbolic tangent with the VLE bulk densities as limits.

3. We solve the DFT equations to yield the equilibrium density profile and calculate the surface tension.

For the VLE, we use the PhaseEquilibrium.pure method. Here for \(T = 300\) Kelvin.

vle = PhaseEquilibrium.pure(pcsaft, 300*KELVIN)
vle

	temperature	density
phase 1	300.00000 K	1.51670 mol/m³
phase 2	300.00000 K	55.38975 kmol/m³

Next, we initialize the density profile. For the surface tension, a 1D DFT calculation in Cartesian coordinates is conducted. Thus, the density profile will be an 1D array (we have a single substance).

To solve the DFT equations, the density has to be discretized which can be controlled by n_grid, the number of grid points. The surface tension is not very sensitive w.r.t the number of grid points but you should make sure to pick a large enough value. When in doubt, run multiple calculations varying the number.

We also have to provide a width of the calculation domain, l_grid. The domain should be large enough that the bulk densities can be observed in the limits. You can check the resulting density profile to make sure that’s the case.

The critical temperature is used to come up with a good initial estimate for the density profile.

%%time
interface = PlanarInterface.from_tanh(
    vle=vle,
    n_grid=512,
    l_grid=100*ANGSTROM,
    critical_temperature=cp.temperature
)
initial_density = interface.density

CPU times: user 89 µs, sys: 137 µs, total: 226 µs
Wall time: 227 µs

The above method does not yet run a calculation. If we try to extract the surface tension, it will return None. Let’s store the initial density profile for a later comparison.

interface.surface_tension == None

True

To calculate the equilibrium density profile, we have to call the solve() method:

%%time
surface_tension = interface.solve().surface_tension

CPU times: user 31.2 ms, sys: 1.3 ms, total: 32.5 ms
Wall time: 32.4 ms

solve() calculates the equilibrium density profile and returns the PlanarInterface object so that we can readily extract the surface_tension.

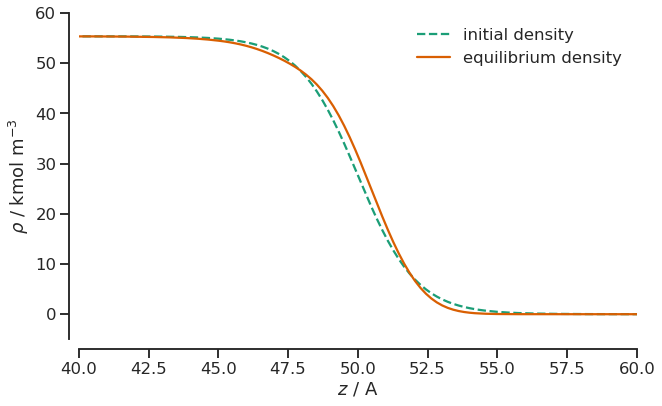
The PlanarInterface.density contains the equilibrated density profile. Let’s compare it to our initial density and zoom into the interesting region between 40 and 60 Angstrom.

plt.figure(figsize=(10, 6))
plt.plot(interface.z / ANGSTROM, (initial_density / (KILO * MOL / METER**3))[0], linestyle="dashed", label="initial density")
plt.plot(interface.z / ANGSTROM, (interface.density / (KILO * MOL / METER**3))[0], label="equilibrium density")

plt.xlim(40, 60)
plt.ylim(-5, 60)
plt.ylabel(r"$\rho$ / kmol m$^{-3}$")
plt.xlabel(r"$z$ / A")
sns.despine(offset=10)
plt.legend(frameon=False);

Comparison to NIST data using SurfaceTensionDiagram

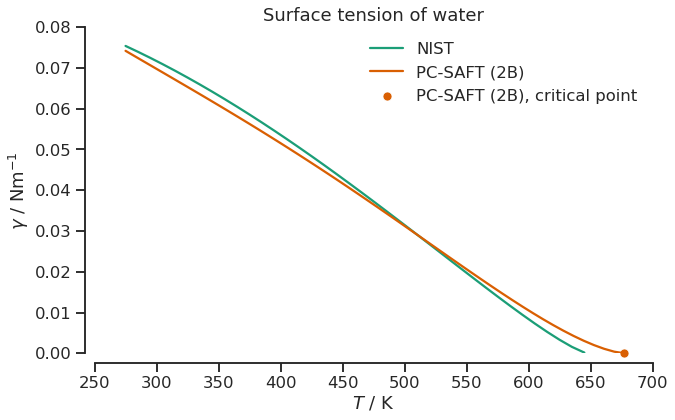
We can use the above steps to calculate multiple VLE’s and then - for each VLE - calculate the surface tension. We provide a utility object, the SurfaceTensionDiagram, that you can use to do exactly this task. Let’s load some experimental (correlation) data obtained from the NIST Webbook and see how the water model compares to that.

literature = pd.read_csv("data/water_vle_nist.csv", delimiter="\t")
literature.head()

	Temperature (K)	Pressure (MPa)	Density (l, mol/l)	Volume (l, l/mol)	Internal Energy (l, kJ/mol)	Enthalpy (l, kJ/mol)	Entropy (l, J/mol*K)	Cv (l, J/mol*K)	Cp (l, J/mol*K)	Sound Spd. (l, m/s)	...	Volume (v, l/mol)	Internal Energy (v, kJ/mol)	Enthalpy (v, kJ/mol)	Entropy (v, J/mol*K)	Cv (v, J/mol*K)	Cp (v, J/mol*K)	Sound Spd. (v, m/s)	Joule-Thomson (v, K/MPa)	Viscosity (v, uPa*s)	Therm. Cond. (v, W/m*K)
0	275.0	0.000698	55.502	0.018017	0.13978	0.13979	0.5100	75.903	75.915	1411.4	...	3271.50	42.830	45.115	164.06	25.580	33.980	410.33	558.89	8.9986	0.016879
1	285.0	0.001389	55.479	0.018025	0.89678	0.89681	3.2139	75.397	75.533	1454.3	...	1704.30	43.078	45.445	159.52	25.736	34.170	417.48	408.81	9.2941	0.017535
2	295.0	0.002621	55.384	0.018056	1.65110	1.65120	5.8154	74.765	75.361	1487.7	...	934.36	43.324	45.773	155.38	25.898	34.374	424.46	304.01	9.6018	0.018214
3	305.0	0.004719	55.233	0.018105	2.40440	2.40440	8.3264	74.038	75.300	1513.1	...	536.20	43.568	46.099	151.59	26.069	34.596	431.28	231.32	9.9196	0.018918
4	315.0	0.008145	55.034	0.018171	3.15730	3.15750	10.7560	73.235	75.301	1531.7	...	320.58	43.811	46.422	148.10	26.252	34.843	437.93	180.66	10.2460	0.019646

5 rows × 25 columns

For the SurfaceTensionDiagram, we need to provide the VLE’s. We compute those using the PhaseDiagram object (here for 50 temperatures between 275 Kelvin and the critical temperature) from which we get a list of PhaseEquilibriums via the states filed. The SurfaceTensionDiagram is nice, because we can reuse equilibrium density profiles from prior iterations as input for the next iteration. It’s therefore typically faster and more stable than an “naive” implementation by hand.

The SurfaceTensionDiagram takes the same arguments n_grind, l_grid and critical_temperature as discussed above.

%%time
vles = PhaseDiagram.pure(
    pcsaft,
    275*KELVIN,
    50,
    critical_temperature=cp.temperature
)
sfts = SurfaceTensionDiagram(
    vles.states,
    n_grid=512,
    l_grid=100*ANGSTROM,
    critical_temperature=cp.temperature
)

CPU times: user 1.24 s, sys: 3.05 ms, total: 1.24 s
Wall time: 1.24 s

We now can extract all surface tensions via surface_tension as well as the liquid and vapor states via the liquid and vapor getters, respectively. Let’s store the results in a pandas DataFrame to make plotting easier.

dft_data = pd.DataFrame(
    np.array([
        sfts.liquid.temperature / KELVIN,
        sfts.surface_tension / NEWTON * METER
    ]).T,
    columns=["Temperature (K)", "Surf. Tension (l, N/m)"]
)

plt.figure(figsize=(10, 6))
plt.title("Surface tension of water")
sns.lineplot(data=literature, x="Temperature (K)", y="Surf. Tension (l, N/m)", label="NIST")
sns.lineplot(data=dft_data, x="Temperature (K)", y="Surf. Tension (l, N/m)", label="PC-SAFT (2B)")
sns.scatterplot(x=[cp.temperature / KELVIN], y=[0.0], clip_on=False, color=colors[1], label="PC-SAFT (2B), critical point")
plt.ylabel(r"$\gamma$ / Nm$^{-1}$")
plt.xlabel(r"$T$ / K")

plt.xlim(250, 700)
plt.ylim(0.0, 0.08)
sns.despine(offset=10)
plt.legend(frameon=False);

Concluding remkars

Hopefully you found this example helpful. If you have comments, critique or feedback, please let us know and consider opening an issue on github.